Guía de uso - Relatividad Especial - Relatividad General - Visión histórica - Multimedia
Un Paseo por la Relatividad Especial
Guión original facilitado a la FECYT para "Semana
de la Ciencia en los Centros educativos".
Animaciones en revisión, disculpen las molestias.
Animación revisión, disculpen las molestias.
¿Qué pasaría si un día vieran a dos gemelos caminando de la mano, pero uno anciano y otro niño?
En esta charla veremos algunos conceptos de una teoría científica capaz de explicarlo sin necesidad de recurrir a ninguna pócima mágica.
¿Saben cómo se llama esta teoría?
¿Saben el nombre de su autor?
¿Saben cuándo se publicó?
No hablaremos de magia, pero veremos cosas que bien pudieran ser mágicas, por ejemplo algunas propiedades que los científicos han descubierto sobre la luz.
¿Han oído hablar de la doble naturaleza de la luz?
Antes de Einstein, los científicos discutían entre sí sobre si la luz era una onda o una partícula.
¿Saben cómo se llaman las partículas de la luz?
¿Saben a qué velocidad viaja la luz (en el vacío)?
Nota: Existen partículas que, en determinados medios, son más veloces que la luz (aunque no superan la velocidad de la luz en el vacío). En adelante, cuando hablemos de velocidad de la luz será refiriéndonos al vacío.
¿Es bastante veloz? ¿No?
¿Alguién sabe cuanto tiempo tardaron los astronautas en llegar a la Luna?
La distancia media de la Tierra a la Luna es de 384.400 km. Si una astronauta desde la Luna nos enviara una señal luminosa:
¿cuánto tiempo (aproximado) tardaría la señal en llegar a la Tierra? poco más de un segundo.
Podemos decir que la Luna está a más de un segundo luz pero a menos de dos.
Pero sigamos con las curiosas propiedades de la luz. Juguemos un rato con ella y veamos cómo se comporta.
Animación revisión, disculpen las molestias.
Una niña juega en un tren lanzando una pelota a 1 km/hora. Si desde la estación viéramos pasar ese tren a 100 km/hora
¿a qué velocidad veríamos moverse la pelota?¿a 101 km/hora?
Cada niño ve que la pelota se desplaza a distintas velocidades. Podemos decir que la velocidad de la pelota depende del punto de vista.
Si la niña, además, "lanzara" un haz de luz, lo vería moverse a 300.000 km/s.
¿Y nosotros? ¿a qué velocidad lo veríamos? ¿a 300.000 km/s + 100km/hora?
Pues no, lo veríamos igual que ella, a 300.000 km/s...
Eso es lo que dicen los experimentos: la velocidad de la luz es la misma para todos los observadores. El resultado era tan increíble, que los mismos experimentadores creyeron que había algún fallo en el experimento.
Y es que, al contrario que la pelota, la velocidad de la luz NO depende del punto de vista.
Ahora sabemos que el fotón es una partícula muy independiente y muy veloz.
Pero os contaré algo más: según la Teoría de la Relatividad Especial, en nuestro Universo nadie puede ganar una carrera al fotón y si recordáis que la velocidad de la luz era de 300.000 km/s uno puede preguntarse lo siguiente:
¿Hay en el Universo un límite de velocidad? Eso es lo que parece ¿no?
Hemos hablado de la luz y de los puntos de vista. En nuestra vida diaria, a menudo utilizamos esas palabras: "según mi punto de vista", "desde mi punto de vista"...
En Física, colocarse en el punto de vista de otro es muy fácil.
(Se llama a un alumno y a una alumna, se les pregunta los nombres y se les sitúa mirando en sentidos opuestos): X e Y tienen puntos de vista diferentes, X ve la ventana e Y ve la puerta. Si ahora les cambiamos de posición, X verá la puerta e Y la ventana. Ambos están situados en la misma habitación, si la ven de forma diferente es porque tienen puntos de vista diferentes. Pero todos estamos de acuerdo en que la habitación es la misma. Y, además, en cualquier momento pueden intercambiar sus puntos de vista.
...Sin embargo, en otros aspectos de la vida, nos costará más colocarnos en el punto de vista del otro. ¡Eso sí que es díficil! (Pero si pudieramos hacerlo ¿no tendríamos también una visión más amplia de la realidad?)
En el ejemplo de nuestros compañeros, ambos estaban quietos, pero ¿qué hubiera pasado con sus puntos de vista si uno de ellos estuviera viajando en un tren y el otro quieto en la estación? Si X fuera la viajera e Y el jefe de estación. ¿Cómo vería cada uno de ellos el movimiento del farol?
Animación revisión, disculpen las molestias.
Mientras
el tren viaja en la noche, la viajera saluda al jefe de estación
bajando y subiendo un farol. La viajera nos ha pintado cómo
ve ella el movimiento de su farol. Éste es, por tanto, el punto
de vista de ella.
Animación revisión, disculpen las molestias.
El jefe de estación ve el recorrido del farol de forma distinta. El jefe de estación nos ha pintado cómo ve él el movimiento del farol de la viajera.
¿Qué trayectoria es la real? ¿Por qué?
(Algunos alumnos dirán que la trayectoria real es la que observa el jefe de estación, pues consideran intuitivamente que el punto de vista válido es el del que está quieto).
Hemos dicho que el jefe de estación está quieto, pero ¿qué significa estar quieto?
¿La Tierra está quieta?
Ahora mismo nos desplazamos alrededor del Sol a 30 km/s.
¿El Sol está quieto?
El Sol y nosotros con él, nos desplazamos alrededor de la galaxia a 220 km/s.
¿Hay algo quieto en el Universo?
Ver anexo: Velocidad de la Tierra
Entonces, cuando decimos que algo está quieto, ¿qué queremos decir?
El jefe de estación está quieto respecto a la estación. La viajera está quieta respecto al tren.
¿Podemos hablar de velocidad sin decir respecto a qué?
Animación revisión, disculpen las molestias.
Pero volvamos a la estación y demos un farol al hombre...
Cuando las situaciones se invierten, ¿los puntos de vista también? (se puede bromear con que eso es lo que suele suceder en la vida)
Si el jefe de estación respondiera a la viajera bajando y subiendo otro farol ¿qué trayectoría vería el jefe de estación?
Animación revisión, disculpen las molestias.
¿qué trayectoría vería la viajera?
En el siglo XVI, Galileo ya sabía que las trayectorias de los cuerpos dependían del punto de vista, pero daba por supuesto que el tiempo era absoluto, que no dependía del punto de vista.
Pero ¿dependerá el tiempo del punto de vista?
En 1905, Einstein fue el primero en "atreverse" a decir que el tiempo no era absoluto. Pero empecemos por el principio. Por aquel entonces, los científicos creían que había un espacio "fijo" respecto al cual la viajera y el jefe de estación podrían medir su desplazamiento absoluto. A este espacio fijo lo llamaban "éter".
Para tratar de demostrar su existencia lanzaron rayos de luz en diferentes direcciones. Daban por supuesto que los rayos lanzados en la dirección del movimiento de la Tierra irían más veloces que los lanzados en perpendicular, ya que a la velocidad del rayo de luz en esa dirección se le sumaría la velocidad de la Tierra.
Los resultados fueron sorprendentes, la velocidad de la luz era la misma en todas las direcciones. Muchos científicos trataron de interpretar este descubrimiento y la mayoría fracasó por sus propios prejuicios sobre la idea del tiempo.
Einstein no tuvo esos prejuicios y pudo resolver el dilema: afirmó que la velocidad de la luz era constante para todos los observadores, aunque decir esto implicaba admitir que el tiempo dependía del observador. Vamos a verlo con el siguiente experimento mental:
Pero antes quiero saber si sabéis lo que es esto (se muestra un cronómetro).
Crono es una palabra griega que significa "tiempo" (para los griegos, Cronos era el Dios del tiempo). Por eso, a los aparatos que miden (metro) el tiempo (cronos) se les llama "cronómetros".
Pero comencemos el experimento: daremos dos cronómetros idénticos a nuestros personajes y les pediremos que midan el tiempo que tarda el farol del tren en bajar.
La pregunta es: ¿obtendrán la misma medida de tiempo?
Como los efectos de la relatividad del tiempo se aprecian a velocidades como la de la luz, tendríamos que pedirles que movieran el farol a la velocidad de la luz y eso es mucho pedir. Pero vamos a imaginar que en vez de saludarse con el farol utilizan el artilugio que mostramos a continuación (su funcionamiento está descrito en la sección 3).
1. Encendamos el artilugio del tren. 2. Pidamos a la viajera y al jefe de estación que cronometren lo que tarda el fotón en bajar y que nos lo digan.
|
Veamos un esquema de lo que cada uno ve.
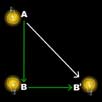El
jefe de estación cronometra AB´
La viajera cronometra AB
Para la viajera, el fotón en el tren va desde A hasta B. Para el jefe de estación, el fotón en el tren va desde A hasta B´. Sabemos que la velocidad del fotón es la misma para ambos. Entonces, ¿el tiempo que medirá el jefe de estación para esta trayectoria será mayor, menor o igual que el tiempo que medirá la viajera?
(Si los alumnos entienden el concepto de velocidad, el dibujo les ayuda a intuir que el tiempo que mide el jefe de estación es mayor que el que mide la viajera).
El jefe de estación ve la trayectoria más larga, por tanto medirá un tiempo mayor.
(Si en vez del artilugio del tren encendieramos el de la estación, pasaría lo mismo pero al contrario. Esta vez, sería la viajera la que vería la trayectoria del fotón de la estación más larga. Con lo que mediría un tiempo mayor que el jefe de estación).
Pero sigamos con nuestro experimento.
¿Podemos utilizar nuestro artilugio como un cronómetro?
Pues sí, un cronómetro da pulsos a intervalos iguales de tiempo y te los muestra en números en la pantalla del visor. En el caso de nuestro artilugio los pulsos son las veces en que se enciende la bombilla. Sólo tenemos que contarlos...1, 2, 3.
Vamos a pedirles que utilicen sus artilugios de cronómetro. Ahora cada uno puede ver el cronómetro (artilugio) del otro y compararlo con el suyo.
Animación revisión, disculpen las molestias.
(Punto de vista del jefe de estación: el jefe de estación
ve que el artilugio en el tren tarda más en completar un ciclo
que el artilugio en la estación. Y que cuanto más veloz
va el tren, más tarda aún en completar un ciclo. En la
animación vemos que mientras el del jefe de estación marca
2 el de la viajera aún está en 1).
¿Por qué se atrasa el cronómetro del tren? ¿Va más lento el tiempo en el tren?
Según el punto de vista del jefe de estación, el tiempo en el tren va más lento.
Animación revisión, disculpen las molestias.
(Punto de vista de la viajera: la viajera verá que mientras su
artilugio marca 2 el del jefe de estación aún está
en 1. La viajera considerará que el tiempo en la estación
va más lento).
Lo mismo le pasará a la viajera, para ella es el tiempo en la estación el que va más lento.
"Cuando dos observadores se desplazan uno respecto a otro a velocidad constante, ambos observan que el tiempo del otro va más lento. Que el reloj del otro atrasa".
Si como demuestran los experimentos, la velocidad de la luz es la misma para todos, tenemos que admitir que el tiempo es relativo, o lo que es lo mismo, que el tiempo depende del observador.
Cuando Einstein publicó su teoría, un periódico vienés encabezó la noticia con el titular: ¡El minuto en peligro!
(Nota: En los ejemplos vistos hasta ahora, nuestros observadores se desplazan a velocidad constante uno de otro y según el Principio de Relatividad las leyes físicas que experimentan son idénticas:
- lo mismo da decir que la viajera se desplaza respecto a la estación que la estación se desplaza respecto a la viajera.
- lo mismo da decir que, según el jefe de estación, el tiempo de la viajera transcurre más lento que al contrario.)
La situación anterior, en la que a los dos observadores les parece que el reloj del otro se atrasa, nos sorprende, pero parece que podemos aceptarla si los observadores se separan indefinidamente con velocidad constante. Sin embargo, ¿qué sucede si los dos observadores se ponen en contacto en un momento posterior y comparan sus relojes de pulsera? ¿A quién se le habrá retrasado el reloj? Este problema suele enunciarse como la paradoja de los gemelos.
Animación revisión, disculpen las molestias.
Uno de los gemelos viaja por el espacio a gran velocidad y al cabo de algún tiempo regresa a la Tierra. A primera vista podríamos pensar que, al igual que en el ejemplo anterior, ambos creerán que el reloj del otro atrasa. Pero en realidad no hay tal paradoja, ya que en este caso uno de ellos ha sido acelerado. La Teoría de la Relatividad Especial da una respuesta inequívoca a la aparente paradoja: cuando ambos se reencuentren, el gemelo acelerado será más joven que el que ha permanecido en la Tierra. Además, experimentos llevados a cabo con aviones y relojes "gemelos" lo han confirmado.
Cada vez que haces un viaje en avión eres un poco más joven que si te hubieras quedado en Tierra. Si tuvieras un hermano gemelo y te despidieses de él para viajar por el espacio a velocidades cercanas a la de la luz, cuando regresaras a la Tierra tu hermano sería más viejo que tú...
Un viaje de ida y vuelta en avión desde Tenerife a la Península hace que envejezcamos una cienmillonésima de segundo menos que si nos hubiésemos quedado en tierra**.
Esta cantidad de tiempo es muy pequeña pero no inapreciable. Utilizando relojes de precisión es posible llevar a cabo una medida de este tipo.
¿Os gustaría viajar al futuro?
En realidad, viajar al futuro no tiene nada de particular. Si queremos viajar al futuro, no tenemos más que sentarnos en una silla y esperar a que llegue.
Pero una nave que nos permitiese viajar al futuro de la Tierra sin apenas envejecer podría ser considerada una "máquina del tiempo".
Bastaría con viajar a velocidades cercanas a la luz y volver al lugar de partida. El problema es que no sabemos cómo construirla, nuestras naves más rápidas viajan a sólo 0,00004 % de la velocidad de la luz.
Sólo os puedo decir que un viaje de este tipo es teóricamente posible. Al menos eso es lo que dice la Teoría de la Relatividad Especial cuyo centenario celebramos este año.
FIN
(*) Einstein desarrolló la Teoría de la Relatividad Especial teniendo en cuenta lo que verían observadores con distintos puntos de vista y dedujo leyes "absolutas" que permiten relacionar las medidas de un observador con las del otro.
(**) Este cálculo es aproximado y se ha realizado sin tener en cuenta otros efectos.