1.3.  Relatividad de Einstein. Suma de velocidades. Tiempo relativo.

Para estudiar la Relatividad de Einstein utilizaremos de nuevo el ejemplo del tren de la sección 1.1 Sobre la plataforma del tren habíamos situado a una viajera que a intervalos regulares de tiempo, t, bajaba y subía alternativamente un farol. Vamos a utilizar el mismo experimento pero, en este caso, “impondremos” que el farol se mueva a la velocidad de la luz

v_y =c

Como no podemos pedir a la viajera que mueva el brazo a la velocidad de la luz, tendremos que inventarnos un artilugio.

Funcionamiento de nuestro artilugio: se colocan dos bombillas, una frente a otra, como se ve en la figura. Dentro de cada una se coloca una célula fotoeléctrica capaz de detectar la luz. En el instante inicial se enciende y se apaga la bombilla superior; un instante, t, después, un fotón procedente de la bombilla superior llegaría hasta la célula fotoeléctrica de la bombilla inferior y la bombilla inferior se encendería y se apagaría; y un instante, t, después, un fotón procedente de la bombilla inferior llegaría  hasta la célula fotoeléctrica de la bombilla superior encendiéndola y, así, se cerraría un ciclo completo.

Aplicando el mismo razonamiento que en la sección dedicada al principio de Galileo (sección 1), el tiempo que tarda para la viajera la luz en moverse de arriba abajo será igual a la trayectoria vertical dividida por la velocidad de la luz (c),

t: duración de medio ciclo según la viajera.

mientras que para el jefe de estación será igual a la trayectoria oblicua dividida por la velocidad de la luz (c’),

t´: duración de medio ciclo según el jefe de estación.

Cuando estudiábamos la Relatividad de Galileo supusimos que el tiempo era el mismo para los dos observadores, t=t’, obteniendo la ley de composición de velocidades de Galileo.

Veámoslo. Según el teorema de Pitágoras

es decir, simplificando el tiempo se obtiene

 

Si aceptamos la hipótesis de tiempo absoluto, la luz debería incrementar su velocidad en el sistema del jefe de estación. Sin embargo, diversos experimentos probaron que la velocidad de la luz era constante, y Einstein decidió romper con el principio de tiempo absoluto.

Ahora, al igual que hizo Einstein, en vez de suponer que el tiempo es absoluto, vamos a aceptar como principio que la velocidad de la luz siempre es la misma, c=c’. Entonces, el tiempo t´que mediría el jefe de estación para el suceso “fotón va de bombilla superior a bombilla inferior (en el tren)” sería mayor que el tiempo t que mediría la viajera para el mismo suceso, ya que la trayectoria oblicua (AB’) es más larga y la luz tardará mas tiempo en recorrerla que la vertical (AB).

Si además el jefe de estación tuviera un artilugio similar, vería como el artilugio del tren se atrasa respecto al suyo.

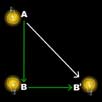
Podemos aplicar de nuevo el Teorema de Pitágoras, pero ahora teniendo en cuenta que el tiempo no es el mismo para los dos observadores y que la velocidad de la luz siempre es la misma, c=c’. En este caso:

ux: velocidad del tren respecto al sistema de la estación.
c: velocidad de la luz.

AB´: trayecto (oblicuo) del fotón según el jefe de estación.
AB: trayecto vertical del fotón.
BB´: trayecto horizontal del fotón.

t: duración de medio ciclo según la viajera.
t´: duración de medio ciclo según el jefe de estación.

Elevando al cuadrado y despejando t en función de t´ obtenemos:

Ésta es la fórmula que expresa la dilatación del tiempo y es consecuencia inmediata de haber considerado que la velocidad de la luz es constante.

Si despejamos t´en función de t:

 

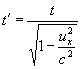vemos cómo, a medida que la velocidad u_x del tren crece, el denominador se hace más pequeño y al jefe de estación le parece que los ciclos son cada vez más lentos. Cuando la velocidad tiende a la de la luz, el denominador tiende a cero y t´ a infinito. Al jefe de estación le parecerá que, en el tren, la bombilla inferior tarda un tiempo infinito en encenderse y pensará que el tiempo de la viajera se detiene.

Pero ¿que pasaría si analizáramos todo lo anterior desde el punto de vista de la viajera? ¿A qué conclusión llegaríamos si fueramos la viajera?