Guía de uso - Relatividad Especial - Relatividad General - Visión histórica - Multimedia
![]() RELATIVIDAD ESPECIAL
RELATIVIDAD ESPECIAL
CHARLA
I - CHARLA
II - SECCIONES - ANEXOS
SECCIONES
1. Observadores no acelerados
1.2 Relatividad de Galileo. Suma de velocidades. Tiempo absoluto.
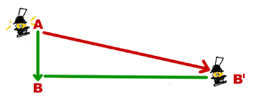
En la sección 1.1 veíamos que la trayectoria seguida por el farol en el sistema de referencia de la estación era la hipotenusa de un triángulo rectángulo: AB’
Si la velocidad del farol en su movimiento vertical es vy, el cateto orientado en esta dirección, AB, tendrá un tamaño: AB=vyt. Si la velocidad del tren es ux, el espacio recorrido en la dirección horizontal (el otro cateto, BB’) será: BB’=uxt. Y la distancia recorrida por el farol (la hipotenusa) será, de acuerdo con Pitágoras,
También podríamos haber dicho que el camino recorrido por el farol en el sistema de referencia de la estación, AB’, sería igual a la velocidad del farol en este sistema, v’, multiplicada por el tiempo: AB’=v’t, y:
Y simplificando el tiempo, t, a ambos lados de la igualdad, la velocidad del farol en el sistema de referencia de la estación sería:
Las coordenadas que describen el desplazamiento del farol en el sistema de referencia del tren después de un tiempo t son:
que el desplazamiento del tren en el sistema de la estación es:
y que el desplazamiento del farol en el sistema de la estación es:
es decir, la suma (composición) de los desplazamientos del farol en el sistema del tren y del tren en el sistema de la estación.
En general, tanto el farol en el sistema del tren como el tren en el sistema de la estación, podrían moverse en las tres dimensiones del espacio, y las ecuaciones que nos dicen cómo se mueve el farol en el sistema de la estación se escribirían:
Éstas
son las leyes de transformación de Galileo. Parece que las hemos deducido haciendo uso exclusivamente
de la ecuación: espacio = velocidad x tiempo. Esta ecuación es general
y los principios que se deduzcan de ella deben serlo también. Entonces, ¿son
las transformaciones de Galileo las únicas aceptables? Sabemos que no,
que puede haber otras alternativas (como las de Einstein). Luego, ¿qué hemos
supuesto sin darnos cuenta en nuestra deducción que conduce a las leyes
de Galileo? Si volvemos a ella veremos que hemos supuesto que el farol
tarda el mismo tiempo en ambos sistemas de referencia en subir y bajar,
es decir, que el tiempo no cambia entre los dos sistemas de referencia.
Por
este motivo, habría que completar
las leyes de transformación de Galileo incluyendo una ecuación que manifestara
la invariancia del tiempo:
Esto es, el tiempo es absoluto, independiente del sistema de referencia. Durante mucho tiempo, esta suposición pareció tan evidente, que la relatividad de Galileo se aceptaba sin cuestionarla y la ecuación de (no) transformación del tiempo simplemente se obviaba. Si dividimos la expresión anterior para la transformación del espacio por el tiempo, obtenemos la ley de composición de velocidades de Galileo: